Grafik fungsi Sinus Cosinus Canvas Javascript
Sebelum menggambarkannya terlebih dahulu pelajari mengenai fungsi sinus dan cosinus dalam trigonometri. Sewaktu SMA kita sudah mendapatkan trigonometri. Jadi saya tidak akan membahas mengenai trigonometri secara lengkap.
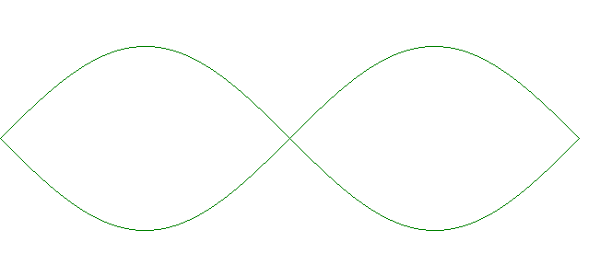
Dalam gambar tersebut grafik sinus ditunjukkan pada puncak pertama. Gambar cosinus ditunjukkan puncak kedua. Fungsi dari grafik sinus dapat ditunjukkan seperti dibawah ini:
f(x) = sin x
Karena umumnya dalam pemrograman menggunakan radian. Kita harus membentuknya dengan radian. Sementara itu fungsi cosinus ditunjukkan seperti dibawah ini:
f(x) = cos x
Dimana x dalam radian. Karena kita akan membentuknya seperti infinity kita melakukan sedikit perubahan pada fungsi cosinus ini. Bagaimana cara kita menggeser grafik cos supaya terbentuk hasil yang diinginkan. Untuk menggesernya kita hanya perlu menambahkan x dengan sudut yang diinginkan dalam hal ini kita menggunakan sudut 90 derajat atau pi/2. Fungsi yang kita gunakan akan berubah seperti ini:
f(x) = cos (x + pi / 2)
Setelah mengetahui fungsi dari sinus dan cosinus kita membutuhkan cara untuk mengubah gradien dunia nyata dengan gradien di komputer. Hal ini dilakukan karena dalam screen komputer tidak memiliki angka negatif. Bagian kanan atas merupakan titik (0, 0) komputer. Semakin kebawah nilai y akan bertambah. Karena itu kita membutuhkan pemetaan sederhana atau yang biasa disebut dengan window to viewport.
Window to Viewport
Window adalah koordinat dunia nyata atau yang biasa kita sebut dengan koordinat kartesius. Sementara itu viewport adalah koordinat elektronik atau koordinat layar pada komputer.
Window mendefinisikan apa yang ingin ditampilkan. Pemetaan bagian dari koordinat dunia nyata ke koordinat device sering disebut dengan window to viewport transformation atau windowing transformation.
Langkah-langkah transformation
- Buat world-coordinate scene menggunakan pemodelan dan transformasi koordinat
- Konversi world-coordinate ke viewing coordinate
- Petakan viewing coordinate ke normalized viewing coordinate menggunakan spesifikasi window-viewport
- Petakan normalized viewing coordinat ke koordinat device
Viewport biasanya didefinisikan dalam bentuk persegi panjang atau square. Namun bisa juga dengan membuatnya menjadi lingkaran atau bentuk lainnya.
Lihat gambar diatas, window dengan viewport memiliki perbandingan yang sama antara jarak titik dan panjang atau lebar titik. Dalam matematika waktu smp kita telah belajar mengenai perbandingan. Dengan cara ini kita dapat menentukan letak titik pada device atau komputer.
Titik di posisi (xw, yw) pada window dipetakkan di posisi (xv, yv) pada viewport. Agar posisi relativ sama gunakan rumus berikut ini.
Dengan sifat matematika didapatkan rumus sebagai berikut :
Setelah saya cek dengan perbandingan rumus diatas ternyata masih salah. Rumus yang benar akan seperti dibawah ini.
Sekarang saatnya kita menggambarkannya dalam source code.
const xv = xvmin + Math.round((xw - xwmin) * (xvmax - xvmin) / (xwmax - xwmin)) const yv = Math.round((ywmax - yw) * (yvmax - yvmin) / (ywmax - ywmin)) - yvmin
Sekarang saatnya kita menggambarkannya dalam source code.
Source code Grafik Fungsi Sinus Cosinus Canvas Javascript
Saya menggunakan ukuran window dan viewport sebagai berikut:
Buat file animation.html dan graph.js isi dengan source code dibawah ini:
Jika sudah hasilnya akan seperti pada halaman ini. click herecanvas.width = 651
canvas.height = 300
const ctx = canvas.getContext('2d')
// window
const xwmin = 0
const xwmax = 7
const ywmin = -1.5
const ywmax = 1.5
// viewport
const xvmin = 0
const xvmax = 700
const yvmin = 0
const yvmax = 300
Buat file animation.html dan graph.js isi dengan source code dibawah ini:
Sekian artikel kali ini. Doain UAS gue lancar wkwk.







Berkomentarlah secara bijak.
EmoticonEmoticon